Untuk yang pernah kuliah di jurusan ilmu komputer pasti sudah tahu dengan materi yang satu ini. Sebenarnya materi ini adalah materi umum yang jurusan-jurusan lain juga mempelajarinya. Hanya saja di jurusan ilmu komputer materi ini akan anda temukan di mata kuliah metode numerik. Berbeda dengan jurusan lain dimana mereka mendapatkannya pada mata kuliah Statistik seingat saya. Juga tidak menutup kemungkinan bahwa jurusan imu komputer pun akan mendapatinya pada mata kuliah Statistik.
Nah, yang masih kuliah sudah ambil belum tuh mata kuliahnya ? Oke, buat yang belum ambil pasti belum tahu kan apa itu regresi ? Kalau begitu mari kita pelajari sedikit tentang regresi dimulai dari pengertian regresi itu sendiri. "Regresi merupakan sebuah metode analisis statistik yang digunakan untuk melihat pengaruh antara variabel bebas dengan variabel tak bebas". Secara umum, regresi terbagi menjadi dua buah yaitu regresi linier sederhana (simple liniear regression) dan regresi linier berganda (multiple liniear regression). Regresi linier sederhana melibatkan 1 buah variabel bebas terhadap sebuah variabel tak bebas. Sedangkan regresi linier berganda melibatkan 1 atau beberapa variabel bebas terhadap variabel tak bebas.
Pada postingan saya kali ini hanya membahas regresi linier sederhana saja, insya Allah pada postingan selanjutnya saya juga akan membahas tentang regresi linier berganda. Kita lanjutkan pembahasan selanjutnya mengenai regresi linier sederhana. Regresi linier sederhana diformulasikan dengan model linier berikut :
dimana :
Harga b0 dan b1 dapat dicari dengan rumus berikut :
Untuk lebih jelasnya langsung saja kita coba dengan studi kasus berikut :
Sebagai contoh : Kita ambil studi kasus pada pohon mahoni. Dimana kita ingin mengetahui apakah ada hubungan antara tinggi pohon dengan diameter batang. Pada contoh ini akan diambil sample data sebanyak 8 buah.
Maka harga b0 dan b1 dapat dicari dengan
Didapatlah sebuah persamaan regresi seperti berikut ini :
Dengan artian misalkan diketahui diameter X = 15, maka nilai tinggi pohon Y melalui persamaan regresi diatas didapat :
Untuk selanjutnya kita akan mengukur koefisien determinasi atau R2 dari model regresi yang telah dibuat. R2 itu sendiri merupakan parameter yang digunakan untuk mengukur seberapa besar kemampuan variabel bebas dalam menjelaskan variasi dari variabel tak bebas. Rumus untuk mencari R2 adalah sebagai berikut :
Sehingga dapat diambil kesimpulan bahwa sekitar 78,5% variasi variabel diameter batang pohon dapat menjelaskan variasi dari variabel tinggi pohon mahoni.
Kemudian terakhir kita juga akan menghitung standard error estimate dari persamaan regresi tersebut dengan persamaan berikut :
Standard error yang didapat diatas menunjukkan bahwa penyimpangan data-data terhadap garis regresi cukup kecil yakni sebesar 6,6364 saja.
Sebenarnya masih ada tahapan terakhir dari regresi yakni uji statistik. Uji statistik terdapat dua bagian yaitu Uji t dan Uji F. Karena kedua-dua uji tersebut memakai nilai t-tabel, maka ini akan saya buat terpisah mengingat nilai t-tabel itu sendiri kita harus memanfaatkan library tambahan untuk perhitungannya.
Baiklah, sesudah mengetahui perhitungan manual regresi linier sederhana. Sekarang kita akan masuk ketahap pembuatan aplikasinya.
- Buat sebuah project baru. Nama project tersebut terserah anda namakan dengan apa.
- Lalu buat sebuah kelas dengan nama "SimpleLinearRegression" pada project tersebut.
- Pada kelas tersebut, deklarasi dan inisialisasi terlebih dahulu variabel-variabel berikut ini.
private double x[] = {8,9,7,6,13,7,11,12};// variabel prediktor/bebas private double y[] = {35,49,27,33,60,21,45,51};//variabel respon/tak bebas private double b_0, b_1; private double r_square; private double s_e; private double sig_x, sig_y, sig_xy, sig_x_square, sig_y_square;
- Kemudian buat sebuah method void dengan nama run, dan masukkan kode dibawah ini.
for(int i = 0; i < x.length; i++){ sig_x +=x[i]; sig_y +=y[i]; sig_xy +=x[i]*y[i]; sig_x_square+=Math.pow(x[i], 2); sig_y_square+=Math.pow(y[i], 2); } b_0 = ((sig_y*sig_x_square)-(sig_x*sig_xy))/ ((x.length*(sig_x_square))-(Math.pow(sig_x, 2))); // rumus menghitung nilai b0 b_1 = ((x.length*sig_xy)-(sig_x*sig_y))/ ((x.length*sig_x_square)-Math.pow(sig_x, 2)); // rumus menghitung nilai b0 r_square = Math.pow(((x.length*sig_xy)-(sig_x*sig_y))/ Math.sqrt(((double)(x.length*sig_x_square)-Math.pow(sig_x, 2))* (double)((x.length*sig_y_square)-Math.pow(sig_y, 2))),2); // rumus menghitung nilai R2 s_e = Math.sqrt((sig_y_square-(b_0*sig_y)-(b_1*sig_xy))/(x.length-2));// rumus untuk menghitung standard error Se
- Sebagai tambahan untuk menampilkan hasil regresi buat sebuah method void dengan nama print, lalu masukkan kode dibawah ini didalam method tersebut.
public void print(){ System.out.println("Persamaan regresi : Y = "+b_0+" + "+b_1+" X\n" + "Koefisien determinasi (R2) = "+r_square+"\n" + "Standard error (Se) = "+s_e); }
- Untuk menjalankan algoritma yang sudah dibuat. Pada kelas SimpleLinearRegression.java buat sebuah method main dan masukkan kode dibawah.
SimpleLinearRegression slr = new SimpleLinearRegression(); slr.run(); slr.print();
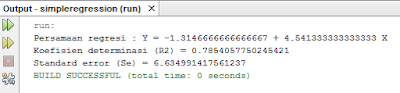
- Jalankan aplikasi, dan hasil yang didapat kurang lebih seperti gambar dibawah ini.
Demikianlah tutorial pembuatan aplikasi Simple Liniear Regression Menggunakan Java. Jika ada pertanyaan mengenai tutorial diatas, silakan bertanya melalui form komentar dibawah. Kemudian jika ingin mengupdate secara rutin artikel yang kami posting dari blog ini, silahkan isi email anda pada Follow by Email dibawah.
Aplikasi diatas bisa diunduh melalui link ini adf.ly/1faiYr.
Terima kasih... wassalam
loading...
0 Comments:
Post a Comment